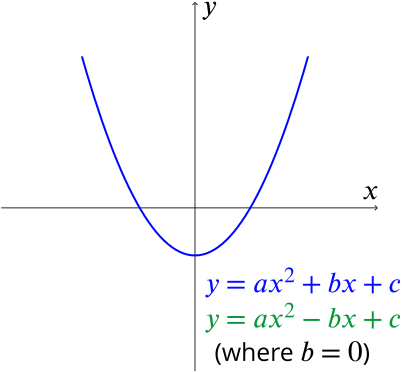
Find an equation of the fom y=ax^2b whose graph passes through the points (1,1) and (2,7) Substitute each x/y pair into the equation so you can solve for "a" and for "b" Graphing y = ax^2 bx c The exception to it not being used as a vertex is when the b is equal to 0 7 How to Find the Vertex y = ax2 bx c The vertex has an x coordinate of –b/2a To find the y coordinate one must place the x coordinate number into the places x occupies in the problem 8X 2 = b Front Porch Math > > Solving Equations of the Form ax2 =b a x 2 = b Example 1 1 18 = 2x2 18 = 2 x 2 Lets start with the equation y = 2x2 y = 2 x 2 If we want to show all the possible solutions we would need to graphing this equation Then we find out that y = 18 y = 18, so the equation becomes 18 = 2x2 18 = 2 x 2
Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt
Y=ax^2+bx+c given points calculator
Y=ax^2+bx+c given points calculator-A free graphing calculator graph function, examine intersection points, find maximum and minimum and much moreSimple and best practice solution for y=axb equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,




Solved The Diagram Shows The Graph Of Y Ax2 Bx C Then A 0 B 0 Self Study 365
B is the coefficient of the x term a is the coefficient of the x^2 term In a straight line, the standard form of the equation is ax by = c where a is the coefficient of the x term b is the coefficient of the y term c is the constant term the slopeintercept form of the equation of a straight line is y = mx b where m is the slopeKCET 19 Permutations and Combinations 3 If 2 x 2 y = 2 x y, then d y d x is KCET 4 Let P = a i j be a 3 × 3 matrix and let Q = b i j where b i j = 2 i j a i j for 1 ≤ i, j ≤ If the determinant of P is 2, then the determinant of the matrix Q is IIT JEE 12 Determinants 5Y = ax^2 b In the system of equations above, a and b are constants For which of the following values of a and b does the system of equations have exactly two real solutions?
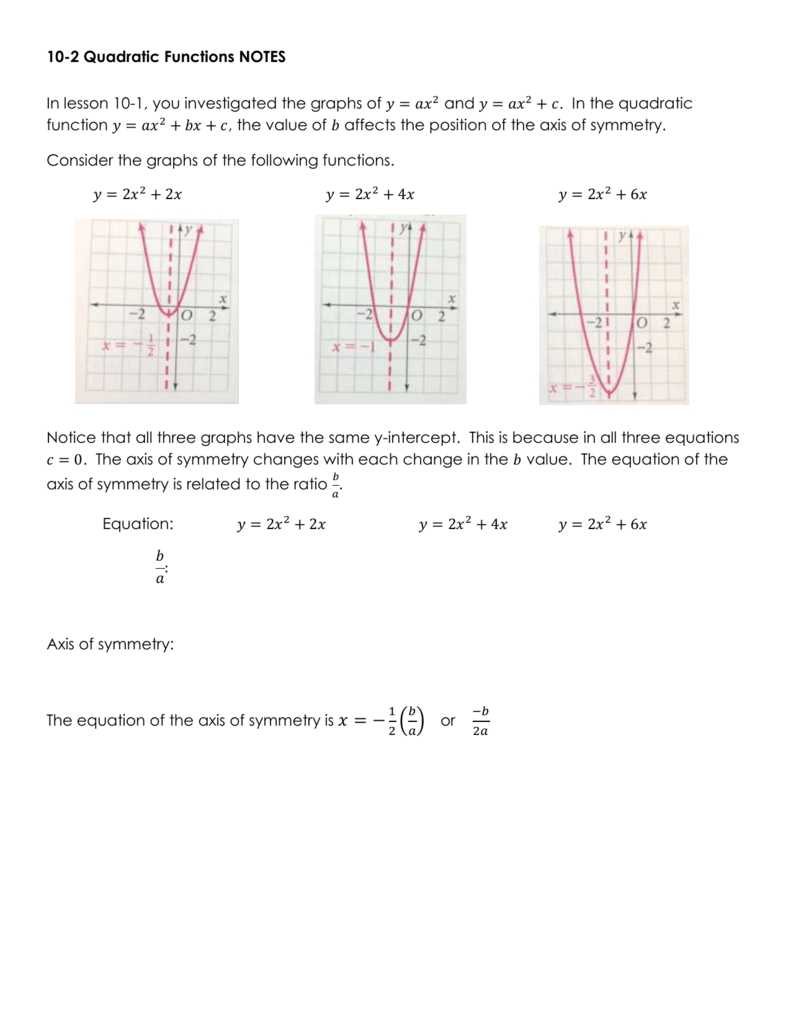
Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byClick here👆to get an answer to your question ️ Given, y = 3 , y = ax^2 b In the system of equations above, a and b are constants For which of the following values of a and b does the system of equations have exactly two real solutions?The vertex of y = a x 2 b x c Set a = 1, b = − 4, and c = 2 to look at the graph of y = x 2 − 4 x 2 Using the formula x = − b 2 a , you can calculate that the axis of symmetry of this parabola is the line x = 2 Also, notice that the vertex of this parabola is the point ( 2, − 2) Now slide c to 45
Graph of y=ax^2k Graph of Try varying the values of k and a and see how it affects the graph of this quadratic function Write down what you see as you change each value of 'a' and 'k' Explain why?Find the quadratic function y = ax^2 bx c whose graph passes through the given points (−1,−3), (3,25), (−2,5) Hint Substitute each point into y= ax^2 bx c to get a system of linear equations, then solve check_circle Adding given equations axbybxay=a^2b^2 (ab)x (ab)y=a^2b^2 (ab) (xy)=a^2b^2 (ab) (xy)= (ab) (ab) xy=ab dome7w and 7 more users found this answer helpful heart outlined Thanks 492
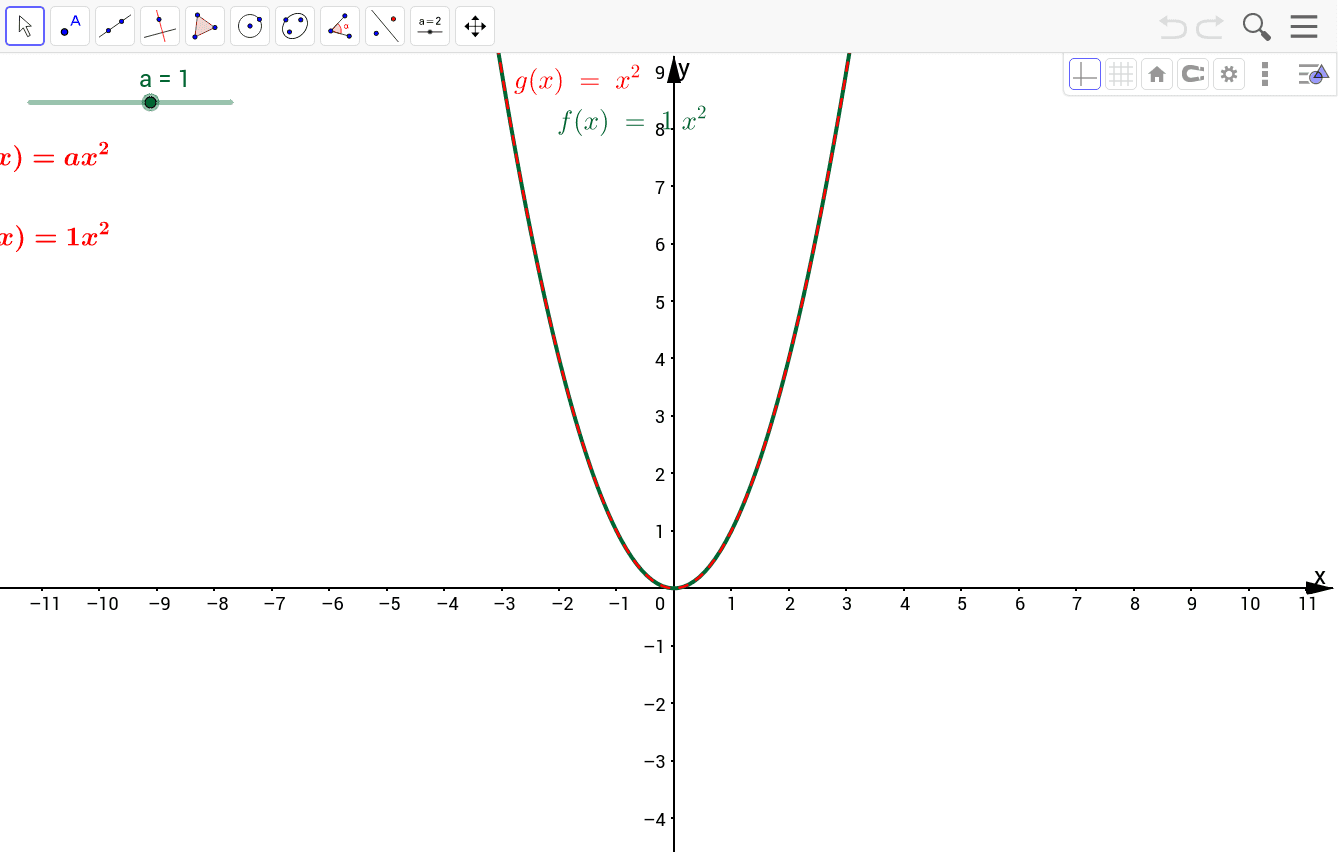



The Properties Of Y Ax 2 Geogebra



Pplato Basic Mathematics Quadratic Functions And Their Graphs
The equation is in standard form x^ {2}a=yb x 2 a = y − b Divide both sides by x^ {2} Divide both sides by x 2 \frac {x^ {2}a} {x^ {2}}=\frac {yb} {x^ {2}} x 2 x 2 a = x 2 y − b Dividing by x^ {2} undoes the multiplication by x^ {2} Dividing by x 2 undoes the multiplication by x 2 y = ax^2 bx^3 is symmetric with respect to (a) the yaxis A graph is said to be symmetric about the y axis if whenever (a,b) is on the graph then so is (−a,b)Calculus questions and answers (d) Show whether y = Ax2 B is a solution for r2 d'y x2 dy x 3y = 0 or not dx2 dx



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora
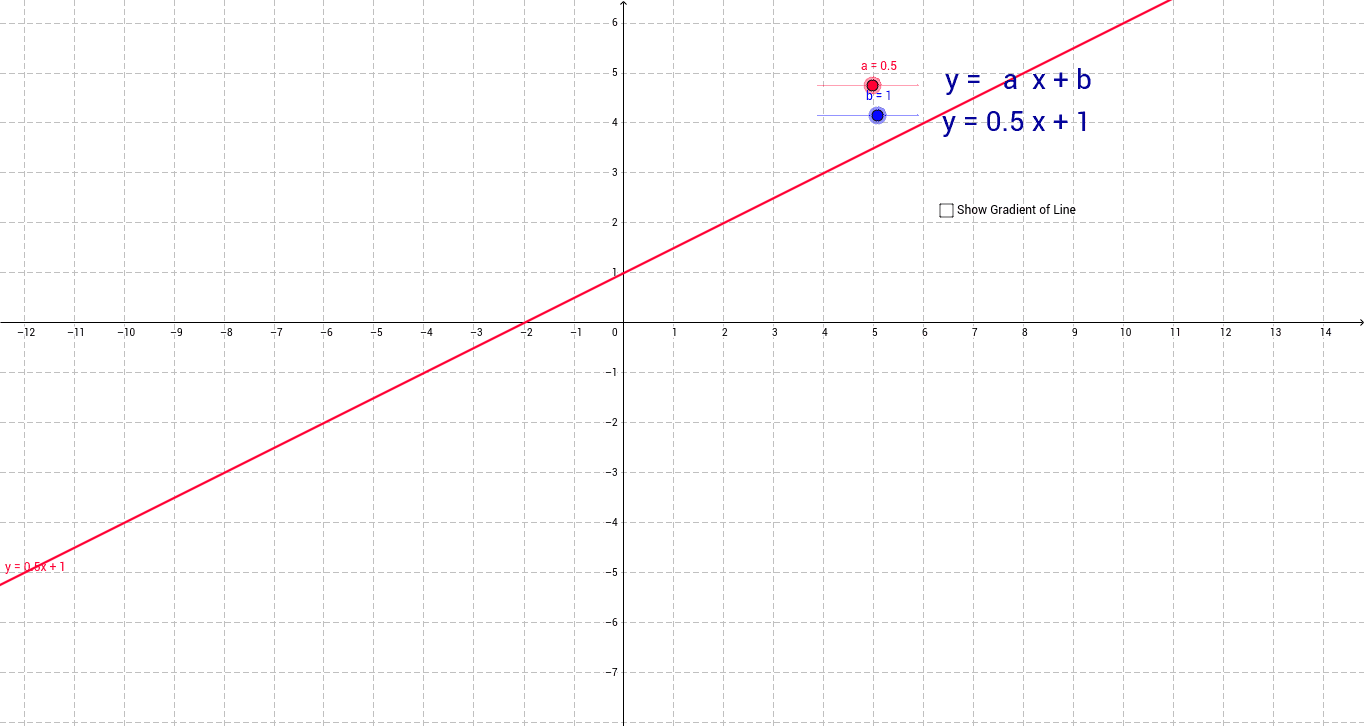



Explore The Effects Of A And B On Linear Graph Y Ax B Geogebra
Click here👆to get an answer to your question ️ If the parabola y = ax^2 6x b passes through (0, 2) and has its tangent at x = 32 parallel to the x axis thenRoots are \ (x = {b \pm \sqrt {b^24ac} \over 2a} \) axis of symmetry isExploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third




The Expression Y Ax 2 Bx C Has Always The Same Sign As Of A If A 4ac Lt B 2 B 4ac Youtube




Clockwise Markers For The Functions Linear Y Ax B Quadratic Y Download Scientific Diagram
SOLUTION y= 3 y= ax^2 b In the system of equations above, a and b are constants For which of the following values of a and b does the system of equations have exactly two real solution Algebra > Realnumbers > SOLUTION y= 3 y= ax^2 b In the system of equations above, a and bThe graph is of the form y = ax 2 The given coordinate is ( 2, 1 ) So x = 2 and y = 1 are on the curve Substitute and solve Parabolas of the form y = a(xb) 2 Example Complete the table of values for the equation y= (x2) 2 Plotting these points and joining with a smooth curve givesExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality



Graph Of A Quadratic Function




Find The Center Of Mass Of The Area Of The Xy Plane Bounded By The Parabola Y Ax 2 And The Line Y B The Area Has A Mass M Study Com
For a = 4 3^05, b = 4 2*3^05 and c = 4 y= ax^2 bx c = (4 3^05)*x^2 (4 2*(3^05))*x 4 b) y= ax^2 bx c has vertex (4,1) and passes through (1,11) 1 = 16a 4b c 11 = a b c the vertex is x = b/2a that is b/2a = 4 by solving the system of equations 16a 4b c = 1 a b c = 11b/2a = 4 we find a = 04Expert Answer Who are the experts?The graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot We say that the first parabola opens upwards (is a U shape) and the second parabola opens




Ch8 Quadratic Equation Solving Methods General Form Of Quadratic Equation Ax 2 Bx C 0 A Quadratic Equation X 2 7x 10 0a B Ppt Download



Observations Of Asymptotic Behavior
Answer to Find the parabola of the form y = ax^2 b which best fits the points (1, 0), (3, 3), (5, 6) by minimizing the sum of squares S, givenWhere a, b, and care constant numbers, and where aand bdon't both equal 0 (If they were both 0 then the polynomial on the left side of the equal sign wouldn't be linear) Examples 3x 2y 7 = 0 is a linear equation 2x= 4y3 is a linear equation It's equivalent to 2x4y 3 = 0,Rewrite the equation as ax2 bx c = y a x 2 b x c = y Move y y to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values a = a a = a, b = b b = b, and c = c−y c = c y into the quadratic formula and solve for x x Simplify the numerator




A Sketch Of Y Ax Bx C Is Shown Brainly Com
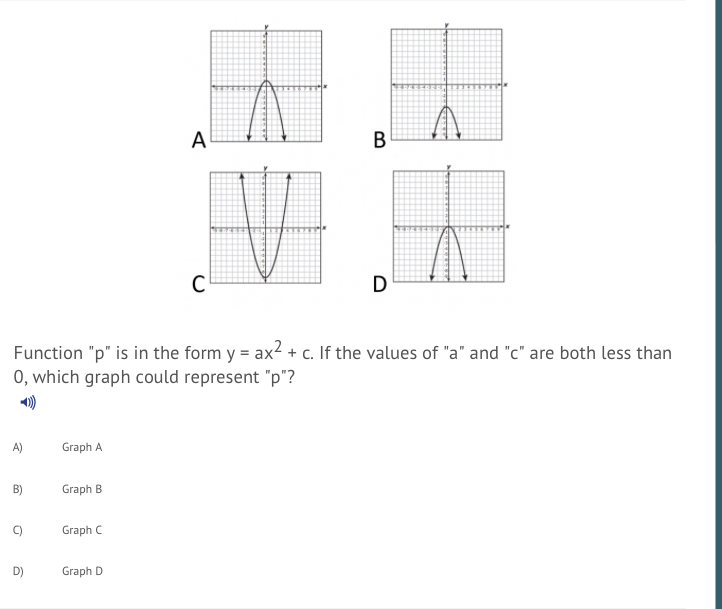



Answered A D Function P Is In The Form Y Ax2 Bartleby
In algebra, a quadratic equation is any polynomial equation of the second degree with the following form ax 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers For example, a cannot be 0, or the equation would be linearLn(y) = A(x)2 B Since this equation has two arbitrary constants, you will have to differentiate it twice to get the required differential equation Differentiating it the first time, (1/y) dy = 2Axdx equation 1 From here, we can get the value of A A = (1/y)dy(1/2xdx) Differentiating equation 1,Find stepbystep Calculus solutions and your answer to the following textbook question The curve y = ax^2 bx c passes through the point (1, 2) and is tangent to the line y = x at the origin Find a, b
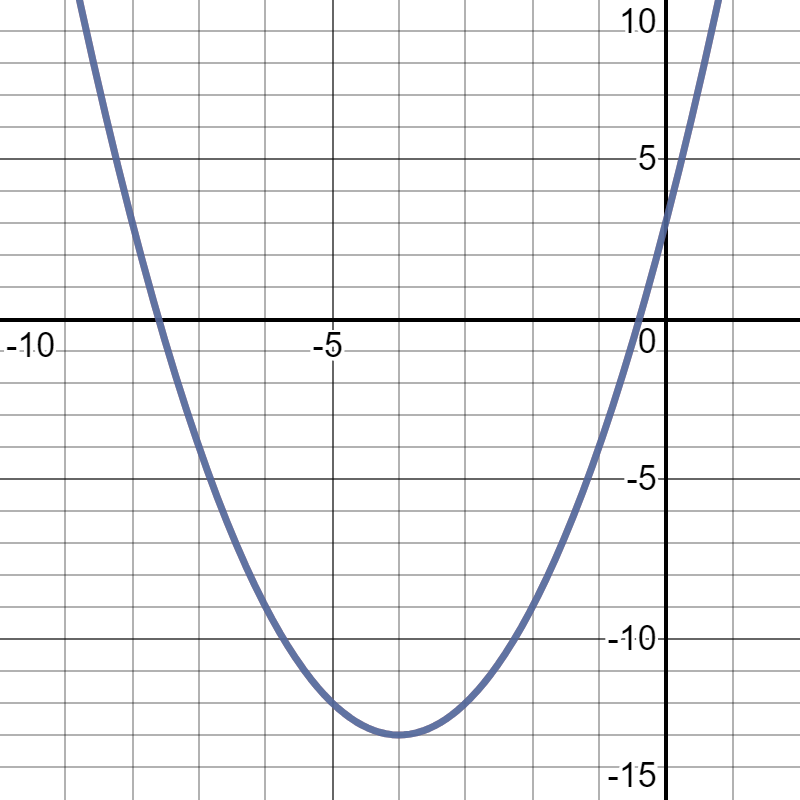



The Equation Of The Curve Is Given By Y X 2 Ax 3 Where A Is A Constant Given That This Equation Can Also Be Written As Y X 4 2 B Find 1 The Value Of A And Of



1
The function y = x 2 ax b is a quadratic polynomial and therefore has one turning point The turning point of a quadratic graph is either the maximum or minimum point The coefficient of x 2 is equal to 1, which being positive implies that this quadratic has a minimum point In order to find the minimum point (assuming existence) of a quadratic polynomial we need to complete the square, y = ax2 bx c ← c is a constant ⇒ dy dx = 2ax2−1 bx1−1 0 = 2ax1 bx0 0 = 2ax bY = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of "a" in front of this space Take half of the coefficient of




Solved The Diagram Shows The Graph Of Y Ax2 Bx C Then A 0 B 0 Self Study 365



Www Humbleisd Net Cms Lib Tx Centricity Domain 3442 Quadratic formula word problems Pdf
Graph y=ax^2 y = ax2 y = a x 2 Find the standard form of the hyperbola Tap for more steps Subtract a x 2 a x 2 from both sides of the equation y − a x 2 = 0 y a x 2 = 0 Divide each term by 0 0 to make the right side equal to one y 0 − a x 2 0 = 0 0 y 0 a x 2 0 = 0 0 Simplify each term in the equation in order to set the rightFor example, a univariate quadratic function has the form f = a x 2 b x c, a ≠ 0 {\displaystyle f=ax^{2}bxc,\quad a\neq 0} in the single variable x The graph of a univariate quadratic function is a parabola whose axis of symmetry is parallel to the yaxis, as shown at right If the quadratic function is set equal to zero, then the result is a quadratic equation The solutions to theAx^2bxc=0 x^2x6=9 x^2x6=0 x^21=0 x^22x1=3x10 2x^24x6=0 quadraticequationcalculator



Quadratics



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora
Try varying the values of a and k and examine what effects this has on the graphSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreIn this video I will show you how to transform the curve y=ax^b into linear form by using logarithms and comparing this to y=mxc, the form of a straight lin




Quadratic Equation Ax 2 B Solution Front Porch Math




Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com
In algebra, a quadratic equation is any equation that can be rearranged in standard form as a x 2 b x c = 0 {\displaystyle ax^{2}bxc=0} where x represents an unknown, and a, b, and c represent known numbers, where a ≠ 0 If a = 0, then the equation is linear, not quadratic, as there is no a x 2 {\displaystyle ax^{2}} term The numbers a, b, and c are the coefficients of the equation and mayAn Exploration of How the Value of the Coefficient a Effects the Graph of the Function y = ax^2 by Margaret Morgan (for College Algebra Students) Arguably, y = x^2 is the simplest of quadratic functions In this exploration, we will examine how making changes to the equation affects the graph ofThere are many differential equations for which mathy(x)=ax^2be^{x}/math is a solution Perhaps the most obvious one is the result of differentiating both side of the equation math\frac{dy}{dx} = 2ax be^{x}/math of course you can the
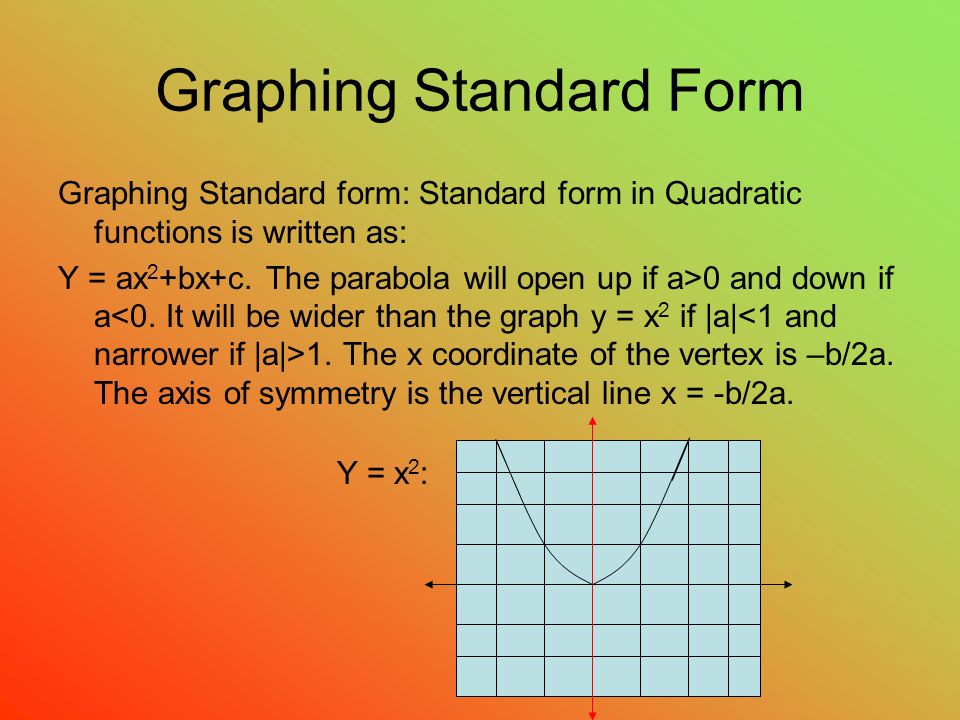



Quadratic Formula Sam Scholten Graphing Standard Form Graphing Standard Form Standard Form In Quadratic Functions Is Written As Y Ax 2 Bx C The Ppt Download



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Sarthaks Econnect Largest Online Education Community
$$y = ax^b$$ $$log(y) = log(ax^b)$$ $$log(y) = log(a) log(x^b)$$ $$log(y) = blog(x) log(a)$$ And furthermore, given two equations rearranged for b $$b = log2(7) log2(a)$$ $$b = log3(8) log3(a)$$5 rows In the next few questions, we will find the roots of the general equation y = a x 2 b x with a ≠ Best Answer #1 2 Suppose that we have an equation y=ax^2bxc whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0) What is (a, b, c)?




Ax2 Bx C 0 Graph Novocom Top
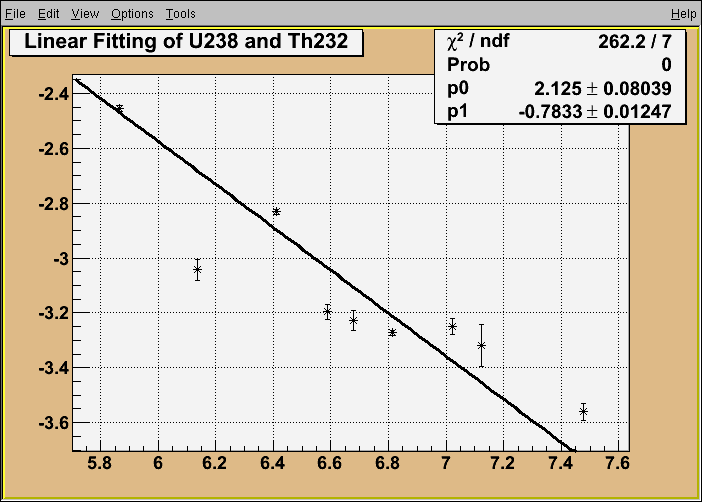



Fitting Linear Y Ax B Covarianc From A And B Root Root Forum
If y=ax^2bx then y'=2axb This gives us our slope of y at any given x So at the point (1,1), the slope must be y'=2a(1)b=2ab We know the slope must also be 3 at the point (1,1), to match the linear equation givenThe Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5Find the parabola of the form y=ax^2b which best fits the points (1,0), (2,2), (4,4) by minimizing the sum, S, of squares of the vertical distances from the above points to the parabola given by S=(ab)^2(4ab−2)^2(16ab−4)^2 Really confused on where to approach this question Could use an explanation if possible, thank you



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
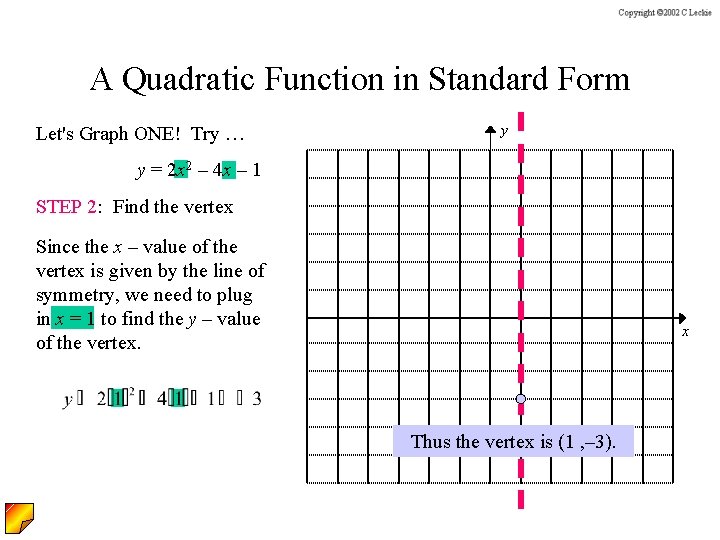



Graphing Quadratic Functions Y Ax 2 Bx C
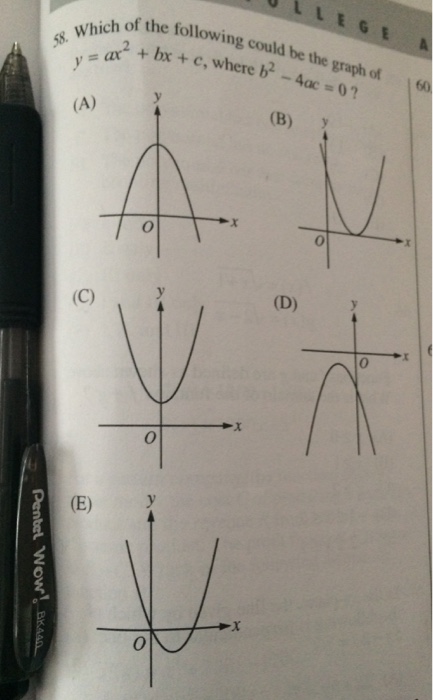



Which Of The Following Could Be The Graph Of Y Chegg Com
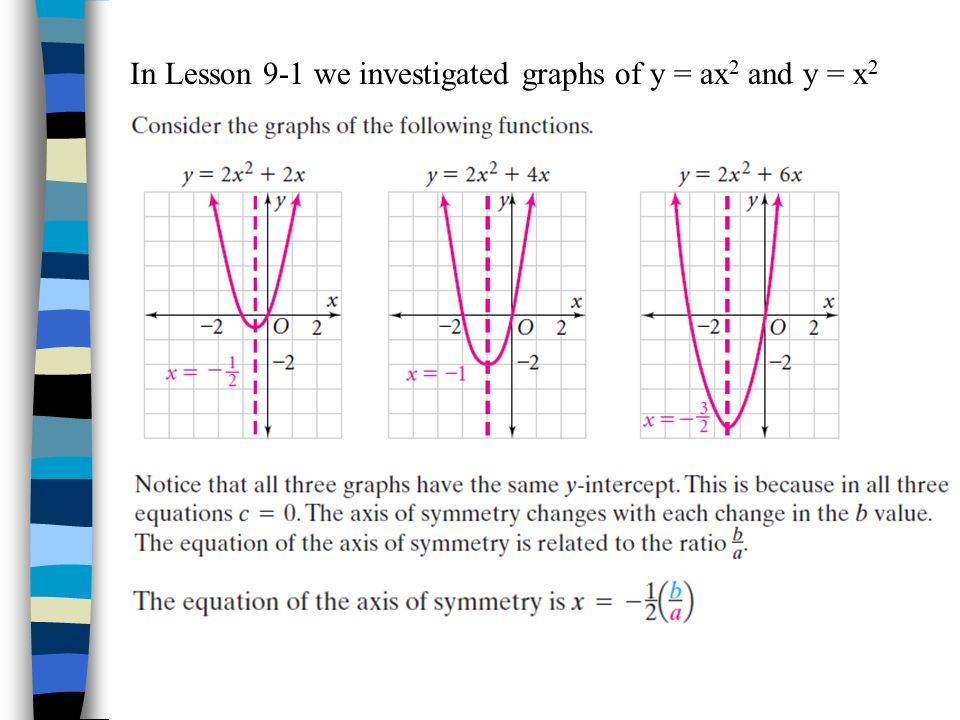



Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download




View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A
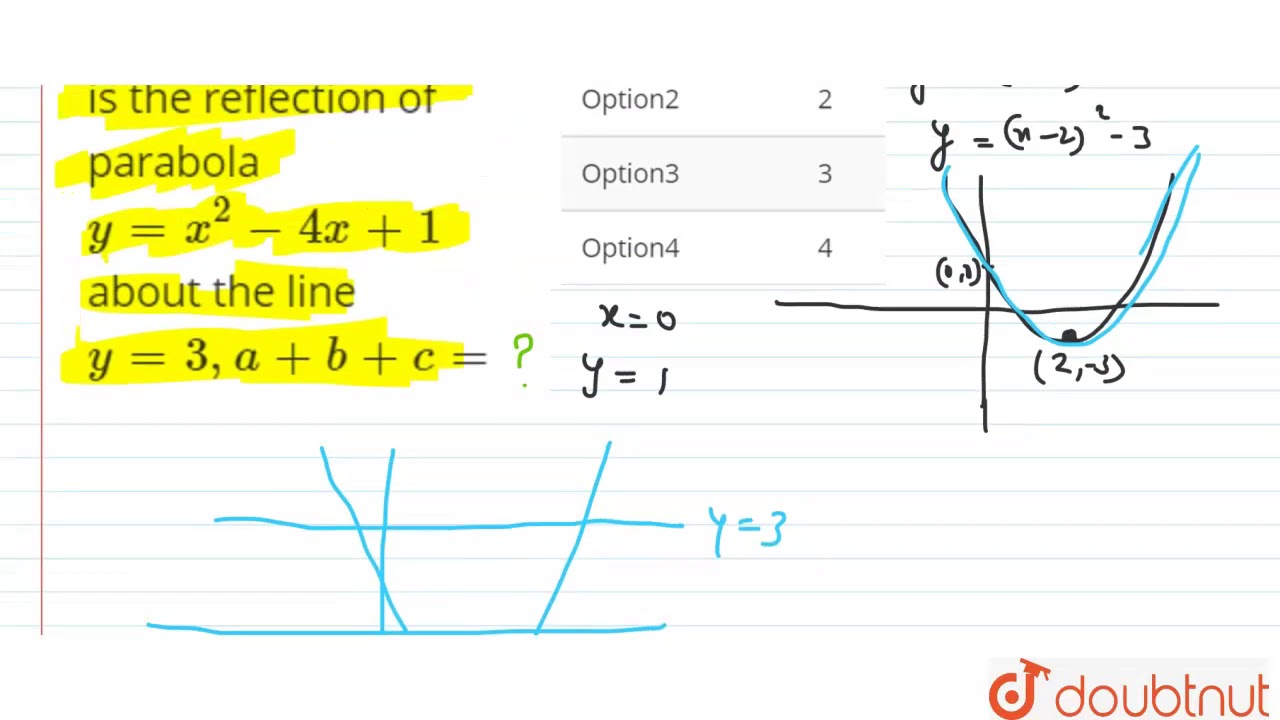



If Y Ax 2 Bx C Is The Reflection Of Parabola Y X 2 4x 1 About The Line Y 3 A B C Youtube




The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com
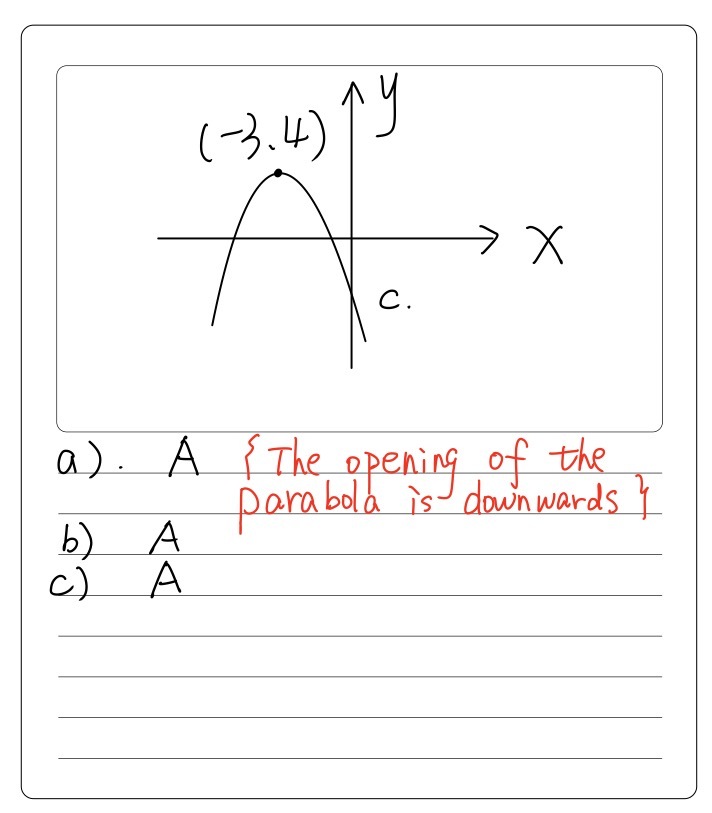



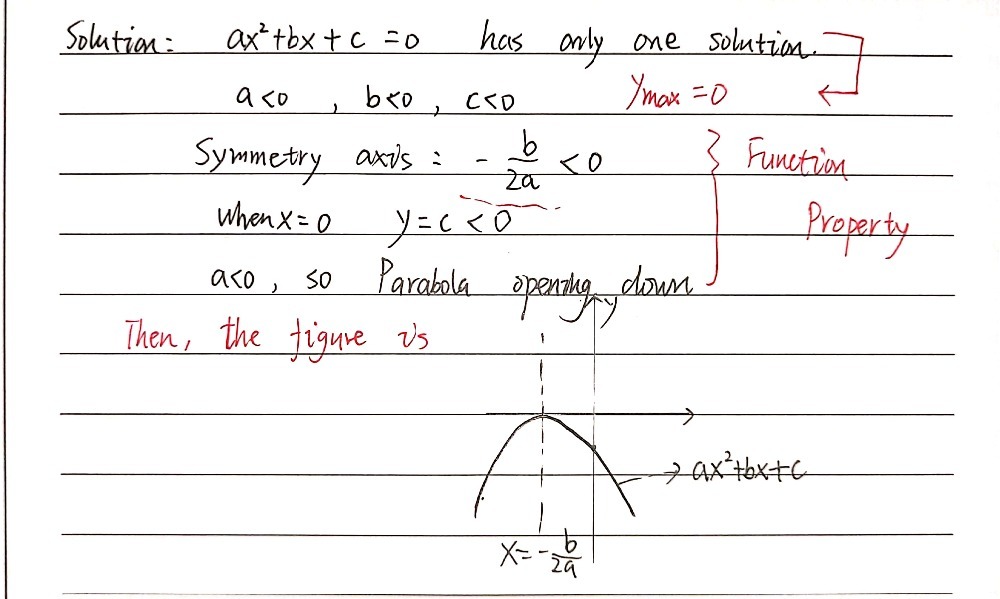
A Sketch Of Y Ax2 Bx C Is Shown B The Maximum Poi Gauthmath



Question 1 Draw A Sketch Graph Of Y Ax2 Bx X Where Gauthmath
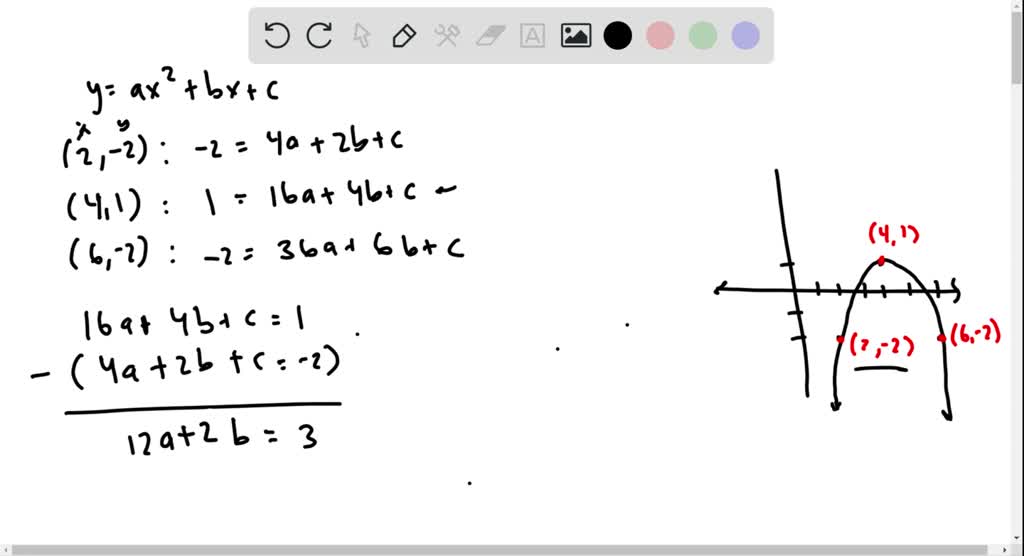



Solved Find The Equation Y A X 2 B X C Whose Gr



Quadratics




Regression Analysis Based On Model Y Ax B Of The Relationships Download Table



1



Http Www Intellichoice Org Wp Content Uploads 16 08 18 Quadratic Functions And Graphs Pdf



If The Parabola Ax 2 Bx C Passes Through The Points 1 12 0 5 And 2 3 Then What Is The Value Of A B C Quora



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola



Quadratics




Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt
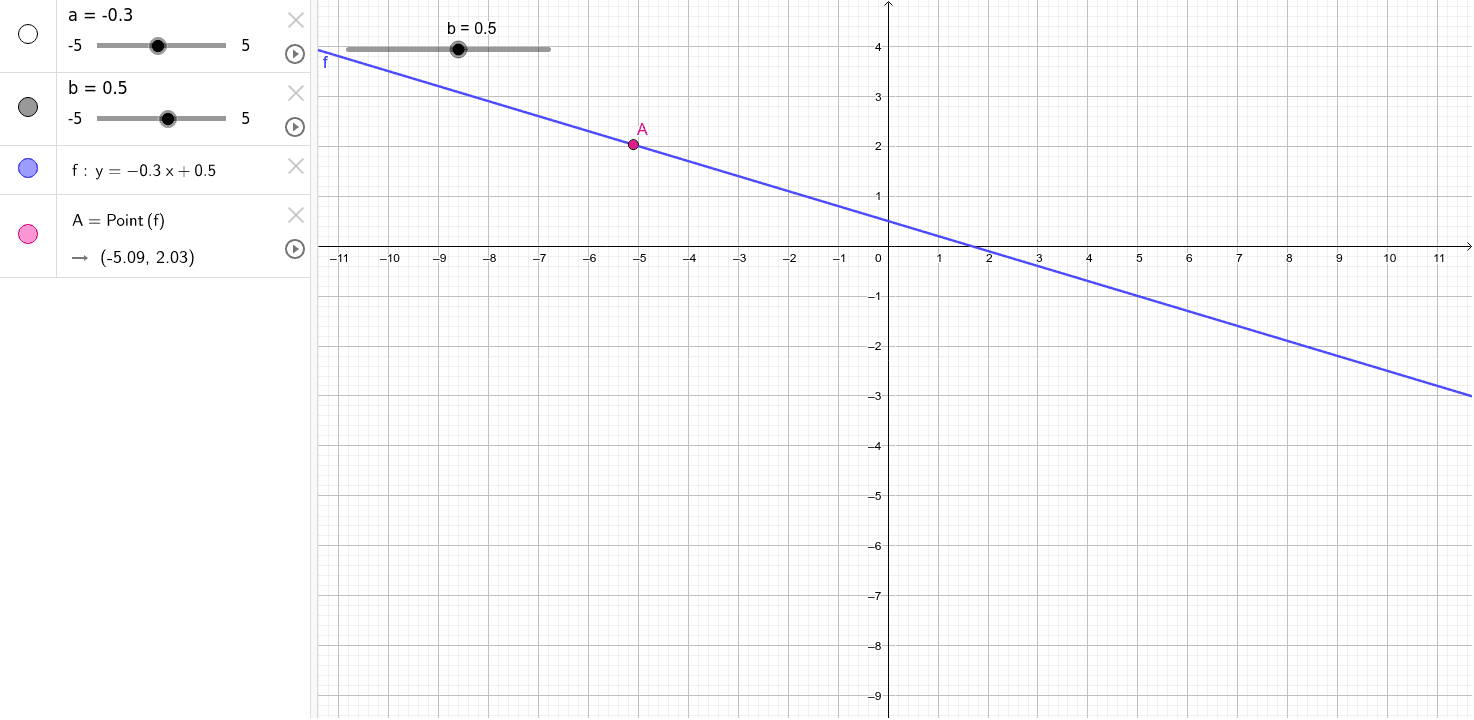



Y Ax B Geogebra




Y Ax 2
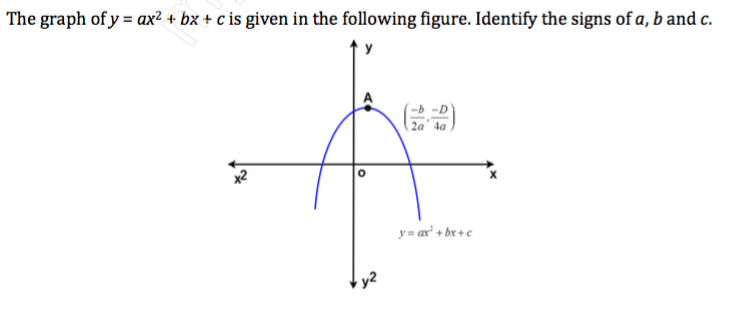



The Graph Of Y Ax 2 Bx C Is Given In The Chegg Com



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau



Solution The Tangent To The Curve Y Ax 2 Bx 2 At 1 0 5 Is Parallel To The Normal To The Curve Y X 2 6x 4 At 2 4 Find The Value Of A And B



Parabola
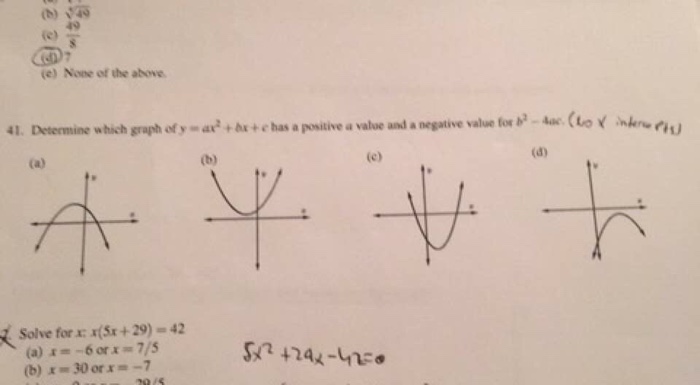



Determine Which Graph Of Y Ax 2 Bx C Has A Chegg Com




What Is The Differential Equation Of The Curve Y Ax 2 Bx
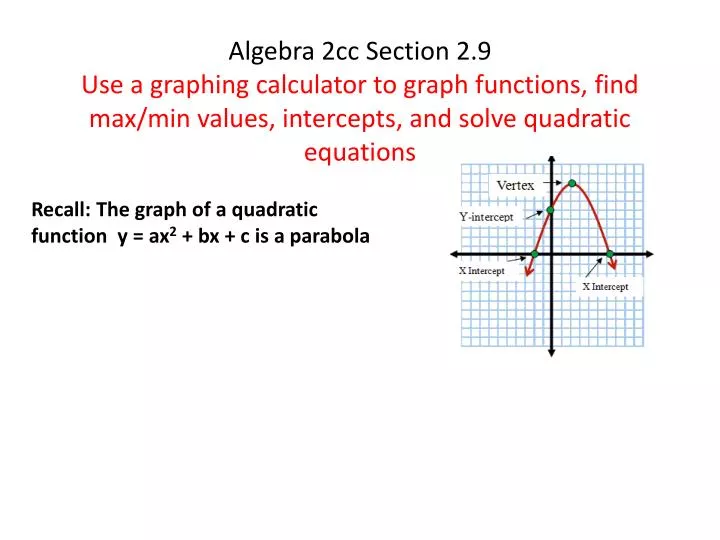



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id



1




Substitute The Coordinates Of The Two Given Points Into Y Ax Ppt Download



Equations And Graphs




Quadratic Functions Y Ax2 Bx C Where A B




Find The Parabola Of The Form Y Ax 2 B Which Best Fits The Points 1 0 4 4 5 8 Mathematics Stack Exchange



How To Find The Equation Of A Curve Y Ax 2 Bx C That Passes Through 1 8 1 2 And 2 14 Quora
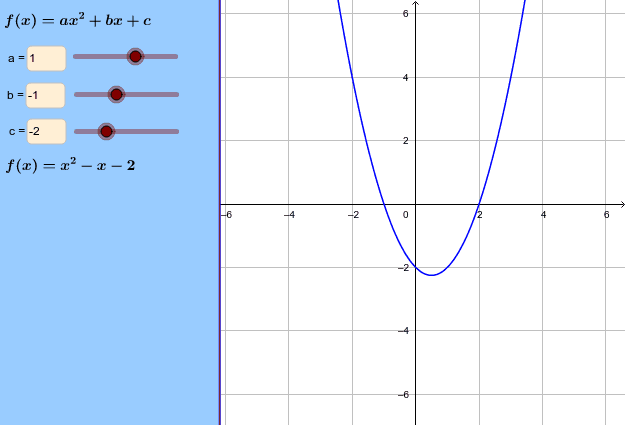



The Graph Of Y Ax 2 Bx C Geogebra



Find The Parabola With Equation Y Ax 2 Bx Whose Tangent Line At 2 4 Has Equation Y 8x Brainly Com
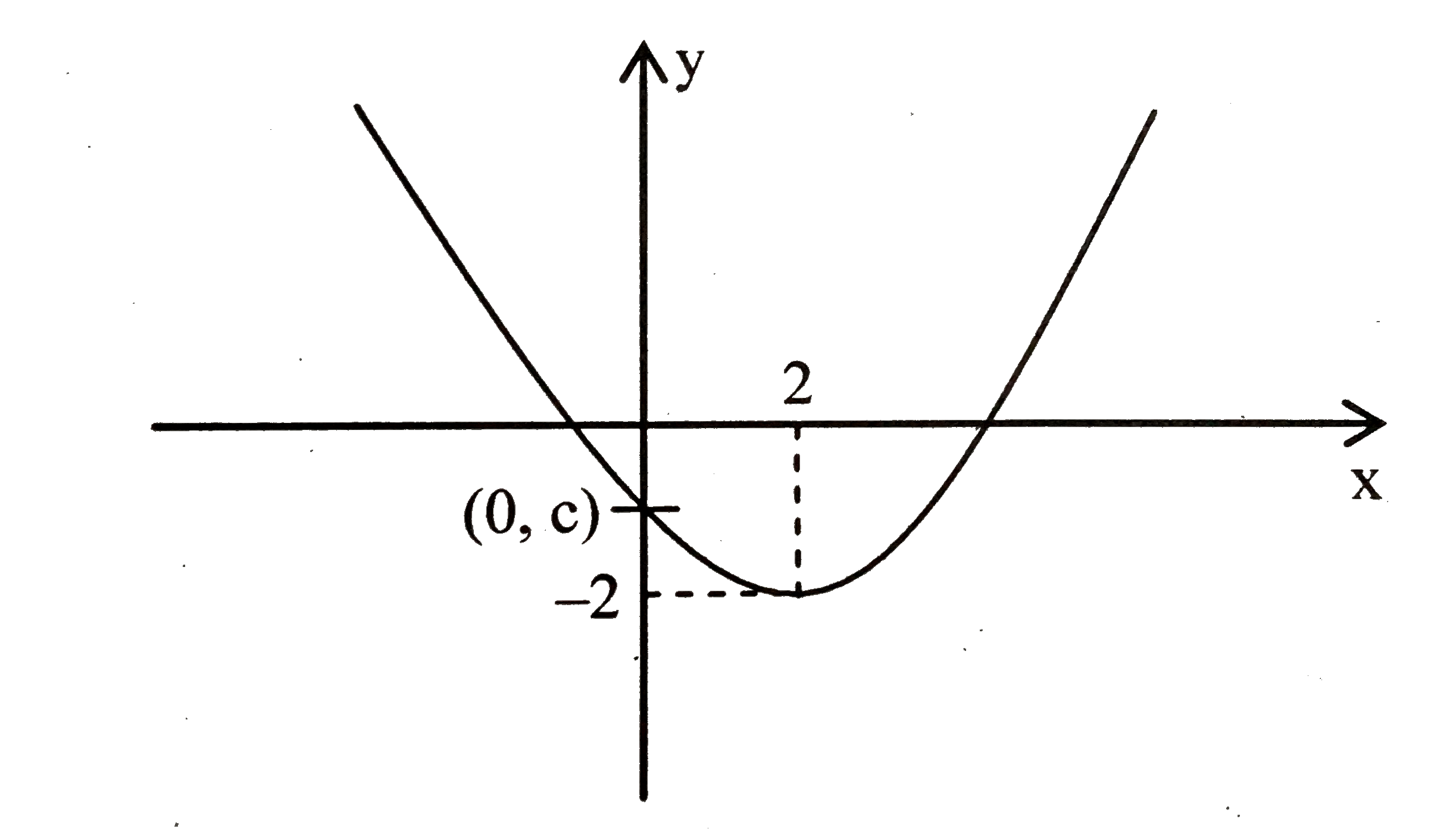



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos



Exploring Y Ax 2 Bx C




Quadratic Function Wikipedia
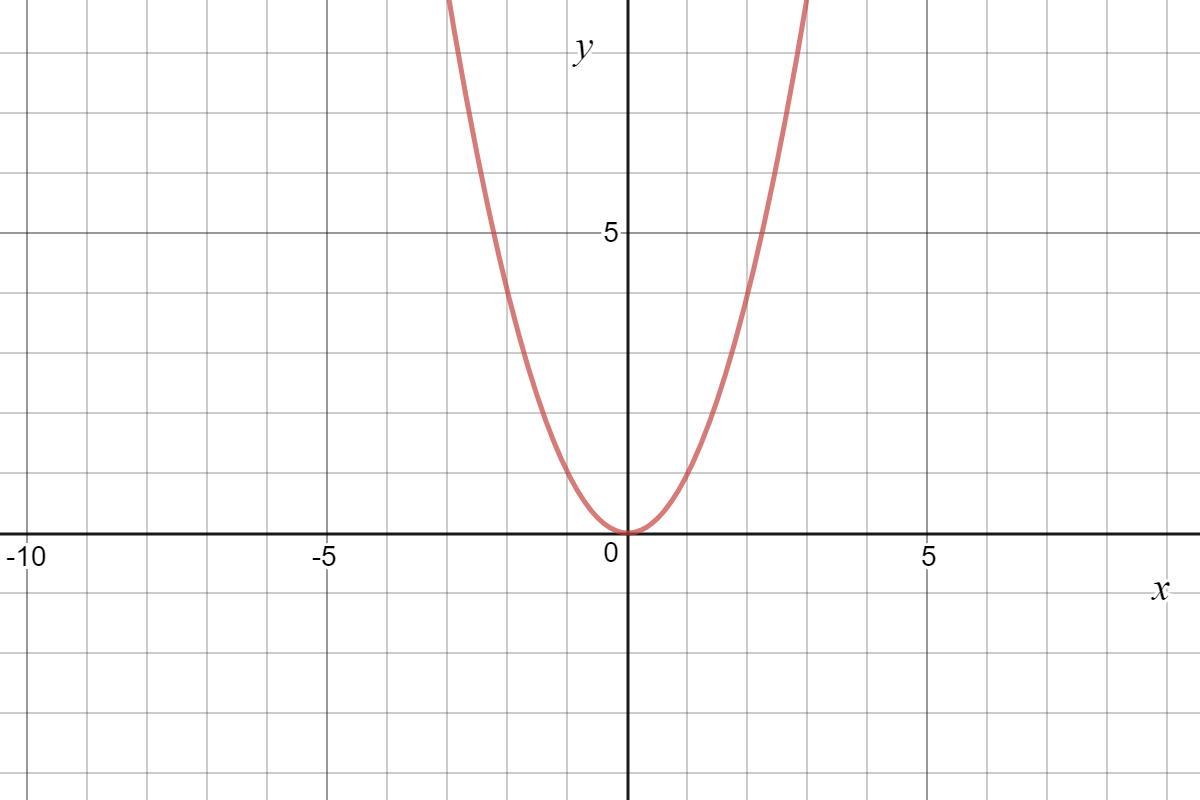



Quadratic Graph Example Y Ax C Expii




Classzone Chapter 4



Quadratics



Exploring Parabolas Y Ax 2 Bx C




Form Differential Equation For Y Ax 2 B Youtube




Quadratic Formula Wikipedia



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com
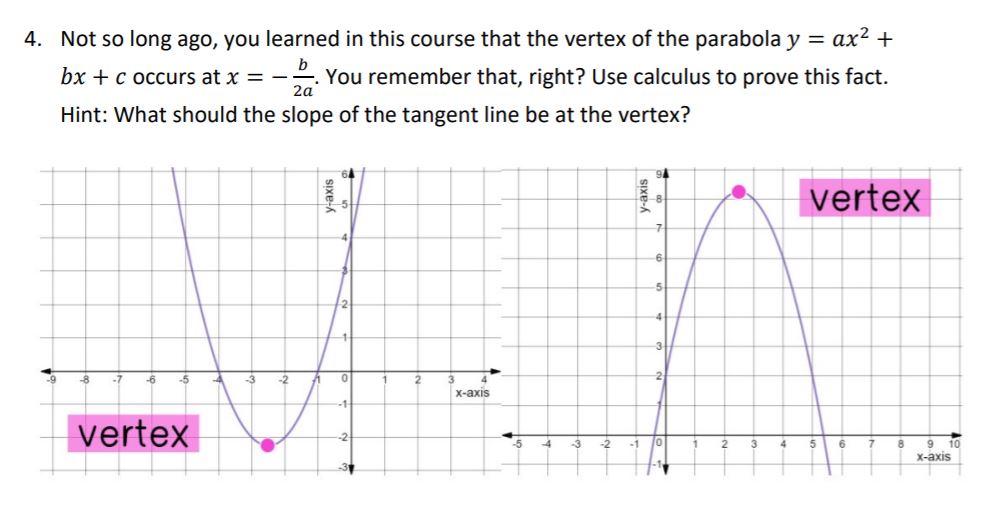



Answered Not So Long Ago You Learned In This Bartleby



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora
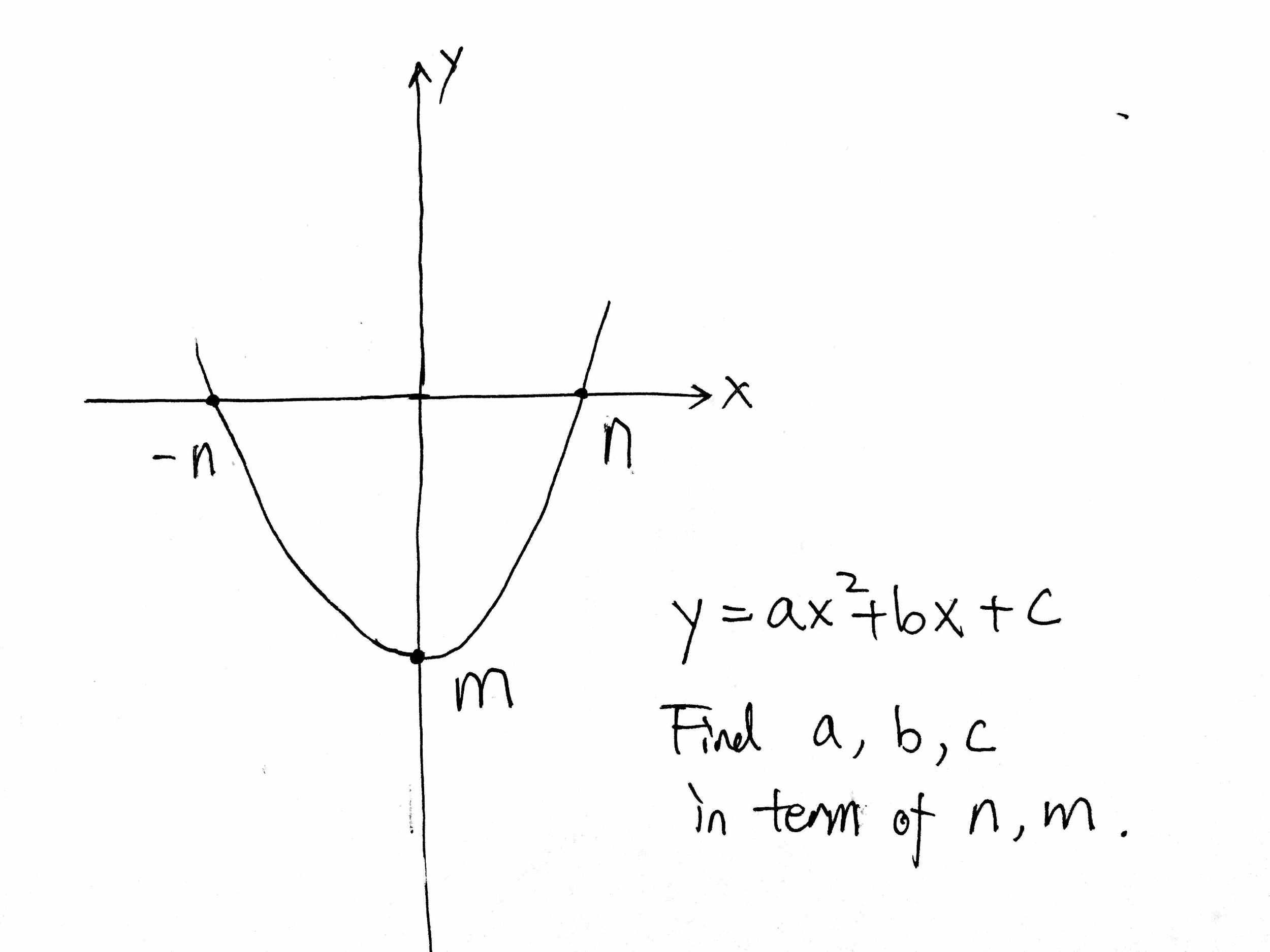



Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com




54 The Graph Of Y Ax2 Bx C Is Shown In The Given Figu Scholr
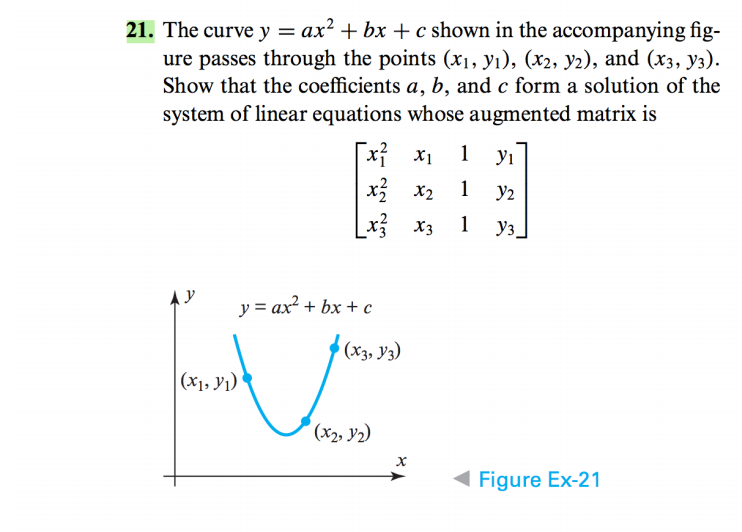



The Curve Y Ax 2 Bx C Shown In The Accompanying Chegg Com



Roots And Coefficients




Non Linear Regression Analysis Y Ax B Of The Relationship Between Download Scientific Diagram



Quadratics



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Graphing Quadratic Functions Ma 912 A 7 1




Graphing Y Ax2 Bx C Youtube



Algebra 1 Activity Sheet Understanding How B Affects The Graph Of Y Ax 2 Bx C



Role Of A B C And D In A Cubic Function Y Ax 3 Bx 2 Cx D Geogebra



Solution Discriminating Quadratics Underground Mathematics



Plot A Graph For The Equation Y Ax Bx 2 Where A And B Ar



Solution Find The Values Of A B And C Such That The Equation Y Ax2 Bx C Has Ordered Pair Solutions 3 23 1 9 And 3 5




Graphing Y Ax 2 Bx C



If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community




Is There A Formula For Finding The Translations Regarding Y Ax B X Askmath




Find The Parabola Of The Form Y Ax 2 B Which Best Fits The Points 1 0 4 4 5 8 Mathematics Stack Exchange




2 Graph Of Y Ax 2 Bx K Graph Of Y Mx K Download Scientific Diagram



Form The Differential Equation Having For Its General Solution Y Ax 2 Bx Sarthaks Econnect Largest Online Education Community
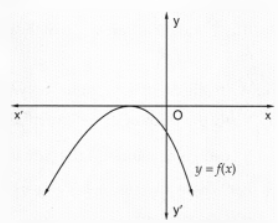



The Graph Of The Polynomial F X Ax2 Bx C As Shown In Fig Write The Sign Of C Snapsolve




Graph Of Y Ax 2 Bx C Novocom Top




If Graph Of Y Ax 2 Bx C Is As Shown Then Which Of The Following Is Correct Where D Equals B 2 4ac




Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download



Algebra 1 Activity Sheet Understanding How B Affects The Graph Of Y Ax 2 Bx C




Y Ax 2 B N Find Dy Dx Maths Trigonometric Functions Meritnation Com
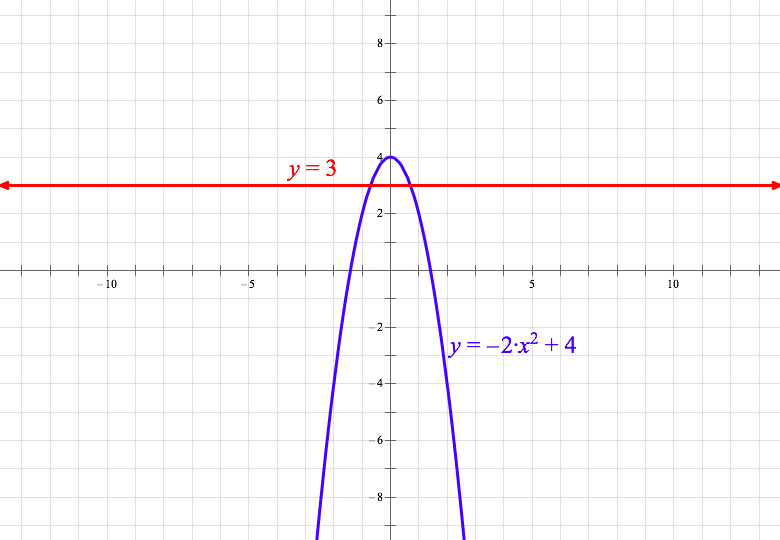



Pwn Test Prep Sat Q A Satpracticetest2 Qn 29 Y 3 Y Ax 2 B In
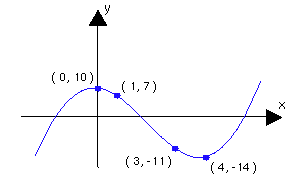



Linear Algebra Webnotes Class Assignments Chapter 1
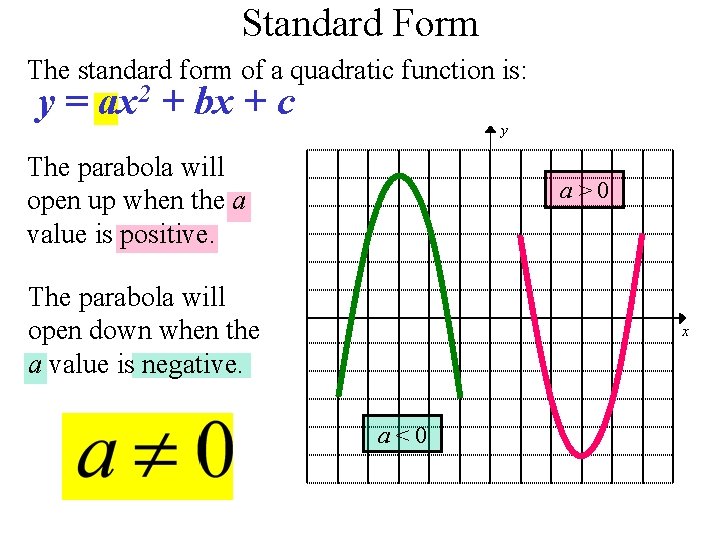



Quadratic Function Y Ax 2 Bx C Quadratic




Quadratic Formula Calculator
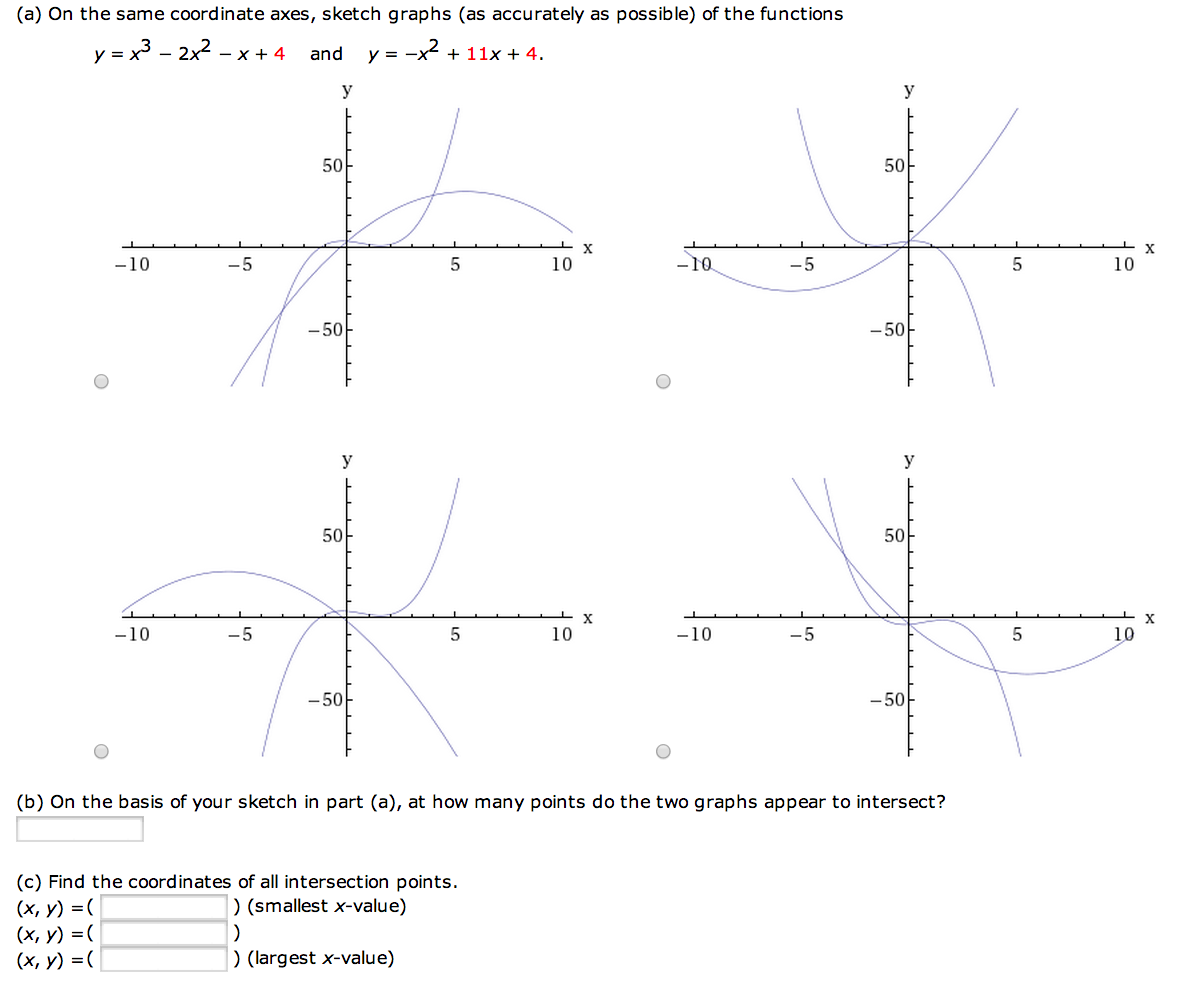



Find A Parabola With Equation Y Ax2 Bx C That Chegg Com




Make X The Subject Of The Formula Y Ax B Youtube
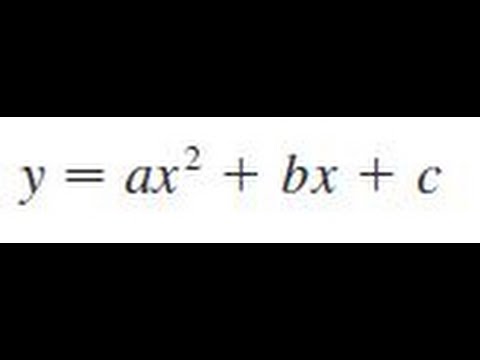



Differentiate The Function Y Ax 2 Bx C Youtube



0 件のコメント:
コメントを投稿